Explaining Differences Between Dummy Coding Values and Effect Coding Values

Two vectors are orthogonal if they are perpendicular to each other. Y 2627 -147 V1393 V2.

Dummy Coding Sage Research Methods

To carry out a comparison of means test or two sample t test between the two groups.

. With dummy coding the estimate of the interaction is fine but main effects are not true main effects but rather what are called simple effects ie the effect of one variable at one level of the other variable. The primary benefit is that you get reasonable estimates of both the main effects and interaction using effect coding. Our example looks like this.

Since X20 for one category of X2 b1 is not a main effect an overall effect of X1 across all values of X2. For the first K-1 levels one recoded variable is equal to 1 eg. The dot product of the two vectors is zero.

When using effect coding the intercept b0 gives the overall grand mean. The difference in coding is that in effect coding the comparison group is identified by the symbol -1. Effect coding is similar to dummy coding.

The difference with orthogonal coding and regression as distinct from the traditional ANOVA approach shown in Figure 714 is that you use the coefficients to populate the vectors just as you do with dummy coding 1s and 0s and effect coding 1s 0s and 1s. Values of effect codings When the coding for White is the omitted Group note that E DD ii 7 where D 7 is the Dummy Variable for White. It is fairly easy just to run a normal regression in R as R automatically know how to code dummies as soon as they are of the type factor.

Dummy coding does not change the general equivalence of ANOVA and regressionthe F tests will be identical. In dummy coding weve set the value of 0 to one of the categories so. The codes variables are now effects codes instead of dummy codes.

0 1 -1 0 is the same as 0 -1 1 0 in that both of these codings compare the second and the third levels of the variable however the sign of the. When there is an interaction the value of b1 eg is the effect of X1 when X2 0. For example let Y be wage and D 1 for female and D 0 for male.

It is not clear to me that using effects coding in the conditional logistic regression context will gain you anything. The regression constant will now represent the average across all groups. Each vector represents a contrast and the values in the vector are the contrasts coefficients each.

These predictors may be coded in three ways. Dummy coding is a way of incorporating nominal variables into regression analysis and the reason why is pretty intuitive once you understand the regression model. 1 0 This hypothesis is rejected when the p-value for ˆ 1 is less than 005.

In this webinar were going to go step-by-step through a few examples of how dummy and effect coding each tell you different information about the effects of categorical variables and therefore which one you want in each situation. Each variable is coded so that it has 1s for one group -1s for the base group and. The standardized slope and significance p-values will be the same for dummy and effect coding as well.

Traditional dummy coding effect coding and orthogonal coding. I would explore using dummy variables created with Statas factor variable notation see the output of help factor variable followed by using the margins command to aid in interpreting your results. No two variables have 1s for the same group.

Effect coding forms orthogonal vectors of the factors RDT subsidy and ACT subsidy while dummy coding does not come with this property. The null hypothesis of two-sample t test says that there is no difference between two groups. Each of the other coefficients give the deviation of the mean of its corresponding group from the grand mean.

However this type of coding also implies that one category from each variable is used as a baseline making it hard to interpret. Effects coding was in general an attempt to get regressions. The decision to code males as 1 and females as 0 baseline is arbitrary and has no effect on the regression computation but.

Regressions are most commonly known for their use in using continuous variables for instance hours spent studying to predict an outcome value such as grade point average or GPA. Each variable has 1s for each case in one group and 0s elsewhere. The R 2 for this model is also 5619.

6069 or Bech and Gyrd-Hansen 2005. We highlight the theoretical equivalence between the dummy and effects coding and show how parameter values from a model based on one normalisation can be transformed after estimation to those. Which level is assigned a positive or negative value is not very important.

To get the mean for each of the groups one could do two regression runs switching the dummy codes of 0 and 1. What is different between the analysis using dummy coding and the analysis using effect coding is the interpretation of the regression coefficients Table 21. Under dummy coding discrete levels appear either as zero or one but under effects coding discrete levels.

For an overview of the issue the reader is referred to Hensher et al. However while this is still the case for the final level of x also for dummy coding with effects coding we additionally set the values for the first K recoded variables to 1. Last we show that the commonly applied multiply by two principle in marginal value calculation under effects coding is theoretically unfounded and offer the correct way moving forward to calculate and interpret welfare measures under effects coding.

For effect coding the effects must sum to zero. This note revisits the issue of the specification of categorical variables in choice models in the context of ongoing discussions that one particular normalisation namely effects coding is superior to another namely dummy coding. A the weights within any contrast vector must sum to zero and b the weights for.

The coefficients reflect actual cell mean differences and have meaningful interpretations as such. While the rule in dummy coding is that only values of zero and one are valid the rule in effect coding is that all of the values in any new variable must sum to zero. Note that regression equation is different.

The estimates are somewhat different however. My professor have told me to just use effect coding instead -1 or 1 as. With the first level D 1 x for dummy coding and E 1 x for effects coding while all others are zero.

R has created a sexMale dummy variable that takes on a value of 1 if the sex is Male and 0 otherwise. It will not be exactly the mean for the entire group because its unweighed as it doesnt take into account the fact that there are different number of individuals into each group. Hence the difference between group 1 and the mean of group means is equal to minus the sum of the estimated effects ie zero minus the sum of the two regression coefficients.

Side By Side Comparison Of Dummy And Effect Coding Dummy Variable D I Download Table

Dummy Coding Sage Research Methods

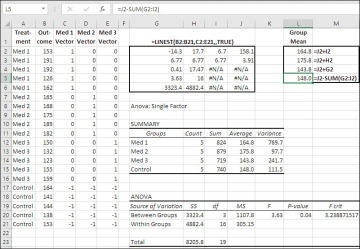
Effect Coding Using Regression To Test Differences Between Group Means Informit

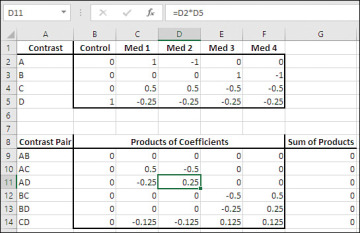
Orthogonal Coding Using Regression To Test Differences Between Group Means Informit

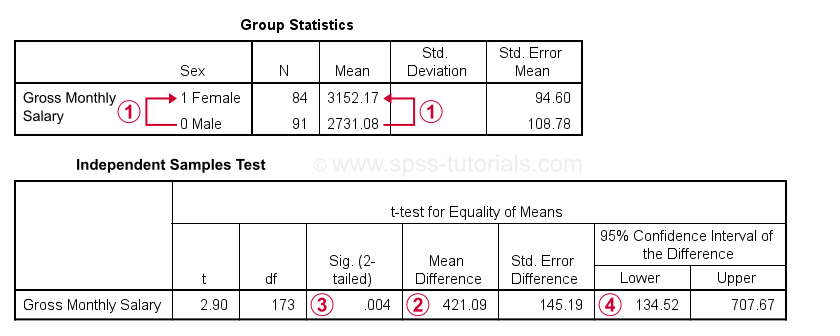
Spss Dummy Variable Regression Examples

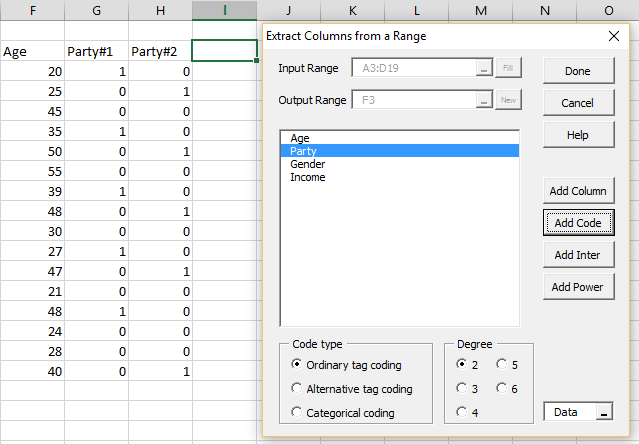
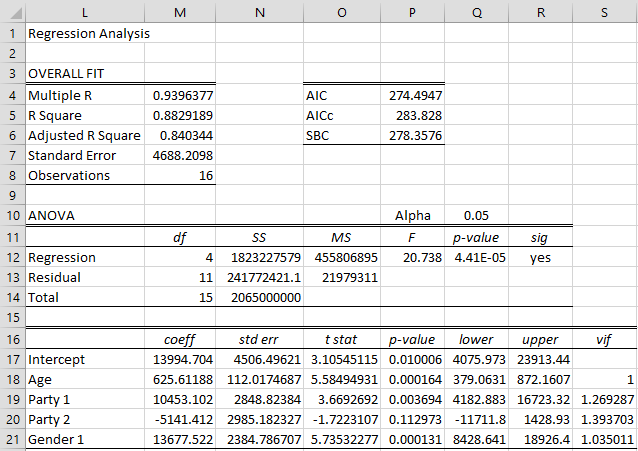
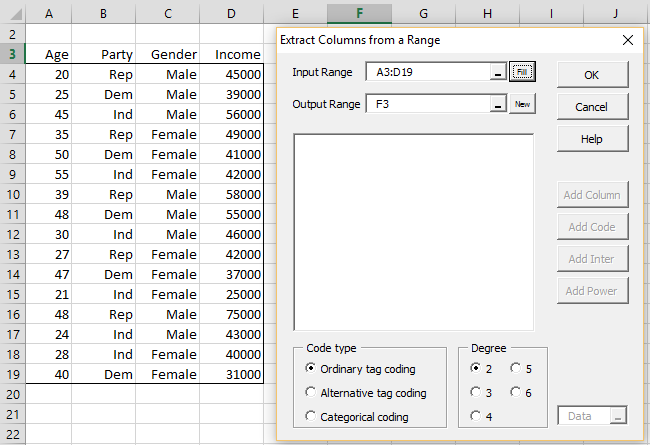
Categorical Coding Regression Real Statistics Using Excel

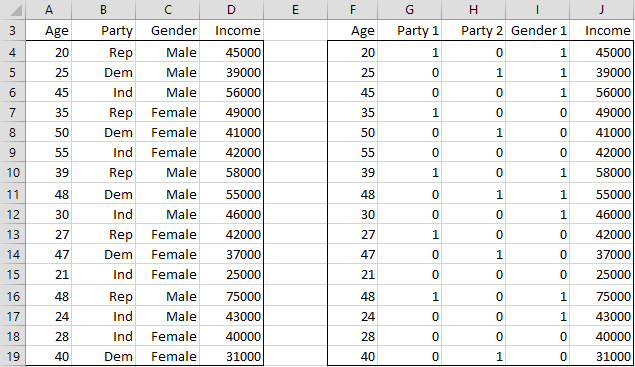
Categorical Coding Regression Real Statistics Using Excel

Dummy Coding Sage Research Methods

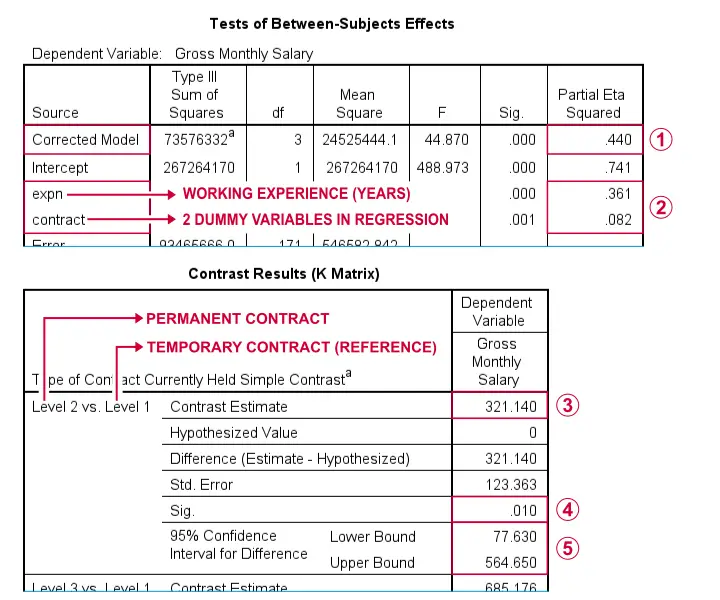
Pdf Categorical Variables In Regression Analysis A Comparison Of Dummy And Effect Coding

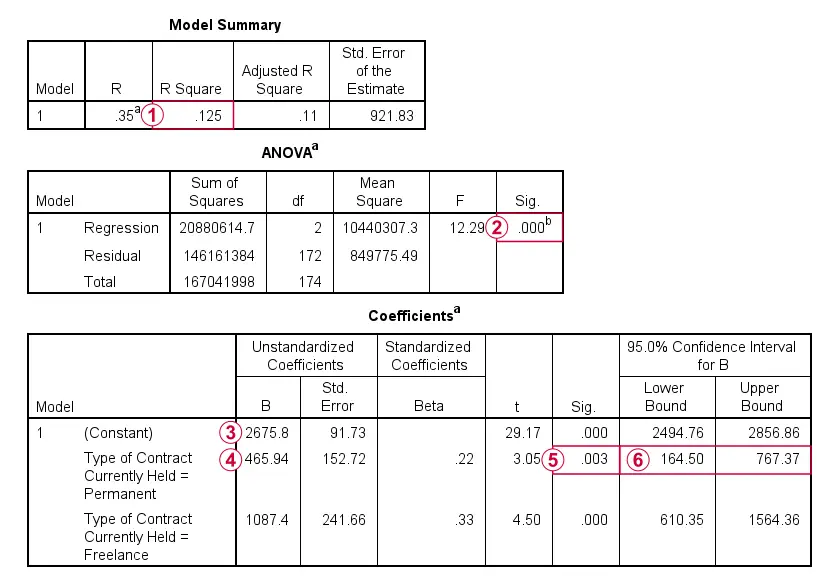
Spss Dummy Variable Regression Examples

Pdf Categorical Variables In Regression Analysis A Comparison Of Dummy And Effect Coding

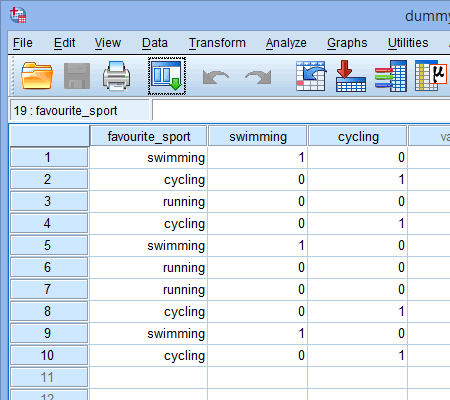
Creating Dummy Variables In Spss Statistics Laerd Statistics

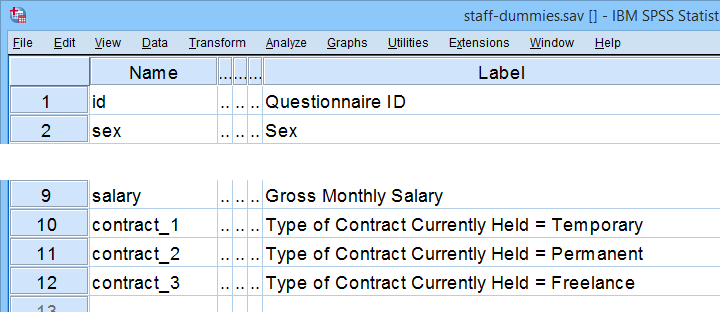
Spss Dummy Variable Regression Examples

Pdf Categorical Variables In Regression Analysis A Comparison Of Dummy And Effect Coding

Categorical Coding Regression Real Statistics Using Excel

Dummy Coding Sage Research Methods

Side By Side Comparison Of Dummy And Effect Coding Dummy Variable D I Download Table

Spss Dummy Variable Regression Examples

Categorical Coding Regression Real Statistics Using Excel